José Manuel Lechado
Periodista y Escritor

La estadística no es una ciencia: es una rama de las Matemáticas que surgió en Alemania a mediados del siglo XVIII. Desde entonces no ha parado de crecer, sus herramientas se han multiplicado y mejorado y su uso se ha extendido a todo tipo de campos, desde la dietética a la física de partículas. Y no es para menos, porque se trata de una herramienta muy potente que, entre otras cosas, sirve para hacer modelos y predicciones muy fiables partiendo de bases probabilísticas y datos no siempre completos. Una capacidad que ha atraído la atención de los poderosos, y su propio nombre ya lo avisa: la estadística (nombre acuñado por el alemán Gottfried Achenwall en 1749) nació como un procedimiento contable para incrementar el control ejercido por el Estado.

Los poderosos son como el rey Midas, pero al revés: todo lo que tocan se pudre. En manos de políticos profesionales, empresarios, banqueros o militares, incluso una rama del conocimiento tan útil como esta se llena de trampas cuando se aplica al oscuro juego de la dominación. Lejos estaba de imaginar Achenwall que su «invento», al cabo de más de dos siglos y medio, iba a servir para manipular la opinión pública hasta tal extremo que hoy no se concibe una campaña política, económica o publicitaria sin un cortejo estadístico destinado a convencer a los ciudadanos de que todo va bien, de que deben votar a tal o cual partido, de que «necesitan» comprar esto o lo otro. Lo que sea.

Pretender que los ambiciosos no hagan fullerías es pensar en lo excusado. No obstante, el lector podrá defenderse mejor de sus engaños si conoce las triquiñuelas que pueden hacerse con las estadísticas. Algunas son burdas, otras ingeniosas y unas pocas, obras maestras. Aunque las fronteras no siempre están claras, las veremos en cuatro grupos: fraudes, planteamiento sesgado, defectos de interpretación y falacias. Esperamos que la descripción de estas añagazas —empleadas a diario por los poderes públicos y privados para deformar la realidad, alterar la información y engañar a los ciudadanos— resulte al lector no sólo útil, sino divertida.

1. FRAUDES

Casi todo el mundo conoce el chiste del pollo: en una población de dos personas, una se come un pollo y la otra no come nada. La estadística local, no obstante, asegura que en la población toca a medio pollo por persona. Este es un fraude estadístico clásico, pero hay muchos más, puesto que se pueden hacer estudios casi sobre cualquier tema a la vez que la inventiva humana para hacer el mal es inmensa.

Levantar una estadística exige reunir datos, ordenarlos de acuerdo a algún criterio y, hecho esto, interpretarlos para extraer conclusiones. En terrenos como la política o la economía una forma habitual de recolectar datos consiste en realizar una encuesta. Su base es lo que se denomina «muestra», es decir, un grupo reducido dentro de una «población». Se da por hecho que la información extraída de la muestra es representativa del total de la población, si bien con un margen de error que varía según el tamaño relativo de la muestra (cuanto más pequeña sea, mayor será este margen). Y aquí es donde pueden empezar las trampas.

Un procedimiento burdo consiste en escoger una muestra demasiado pequeña y mentir en el margen de error (u omitirlo en las conclusiones). Digamos, por ejemplo, que el 90 por ciento de mis partidarios afirman que soy el líder que España necesita. Es reconfortante, y agradezco su apoyo, pero como encuesta no vale mucho si uno tiene sólo cuatro fans.

Antes de seguir es justo recordar que los errores pueden no ser intencionados, y esto tanto en la selección de la muestra como en la determinación del margen de error. Por otro lado pueden influir factores aleatorios y, a veces, incontrolables: si el encuestador es perezoso puede que no le apetezca subir a los pisos más altos de los edificios sin ascensor; y si decide visitar a la gente, cuestionario en mano, a la hora de la siesta, quizá el apartado «No contesta» sume más de lo normal. Estos son problemas metodológicos que, sin ser fraude, alterarán los resultados.

La cosa deja de ser inocente cuando se falsea a sabiendas. No tiene mayor misterio: los datos se elaboran a medida de las conclusiones deseadas, sin hacer encuesta alguna. A pesar de que es fácil descubrir una superchería como esta, se producen de vez en cuando: el falsificador cuenta con la pasividad o la pereza del público a la hora de investigar el origen y veracidad de las conclusiones que se le presentan.

Un fraude de apariencia inocente radica en el anonimato de los encuestados. Recordemos que una estadística basada en encuestas no puede ser anónima: cada persona que conteste debe ser identificada para que la información pueda contrastarse de forma independiente. Pero hay más: incluso encuestas reales, como las que aparecen a menudo en revistas de papel o digitales, carecen de validez si los encuestados no aportan su filiación, porque el anonimato anima a muchos a responder de forma falsa, «imaginativa» o poco rigurosa. No hace falta insistir en cuál es el valor de una estadística que parta de tales premisas. Más aún si, encima, una misma persona tiene la posibilidad de responder varias veces el mismo cuestionario (cosa corriente en Internet). Veamos un ejemplo: una revista ofrece un cuestionario a sus lectores para conocer lo que opinan sobre la publicación. Las conclusiones se presentan bajo grandes titulares en el siguiente ejemplar: «Éxito abrumador. El noventa y cinco por ciento de los encuestados declara que nuestra revista es la mejor del kiosco». Sin duda es así, puesto que sólo han opinado las personas que ya compraban la revista (señal de que les gusta). Pero falta la opinión de los que no la compran (y la de los lectores que no se han molestado en contestar).

La cosa empeora cuando se ocultan datos. Esto no implica que la estadística mienta, pero desde luego no dice toda la verdad, con lo que las conclusiones sí serán fraudulentas. Se comienza por seleccionar los datos que apoyan la hipótesis deseada y se obvia el resto. Por ejemplo, en una estadística (seria) sobre paro, se descubre un repunte de la actividad laboral. ¡Es una buena noticia! El trabajo de campo, sin embargo, ha ofrecido otros datos: que los nuevos trabajadores cobran la mitad que los antiguos o que la duración de los contratos se ha reducido, por término medio, a la cuarta parte del tiempo. Los promotores de la estadística (quizá el gobierno de turno) anunciarán a bombo y platillo la reducción del desempleo y no hablarán sobre ningún otro tema escabroso, como la pérdida de poder adquisitivo o de horas de trabajo.

Otra posibilidad es la interpretación artera de datos no concluyentes. Un estudio puede demostrar que la principal causa de muerte en el mundo son las enfermedades cardiovasculares. Es un hecho cierto e innegable. Sin embargo, esto, por sí mismo, no indica nada. Es posible que haya otra información asociada, como que la mayor parte de la gente que fallece a causa de una de estas enfermedades tiene más de setenta años. A fin de cuentas, cuando uno es viejo ha de morir de algo. En ese mismo estudio se observa que las muertes en accidente de tráfico, aunque abundantes, son muchas menos. Sin embargo, la mayoría de las personas que mueren en un accidente de esta clase son más bien jóvenes. Esto implica factores que no se han tenido en cuenta en las conclusiones (quizá porque el estudio lo financia una conocida marca de medicamentos contra el infarto): que la gente muera joven se asocia a una pérdida de años de vida que, en términos humanos y económicos, es más grave para el común (no para los que pagaron el estudio).

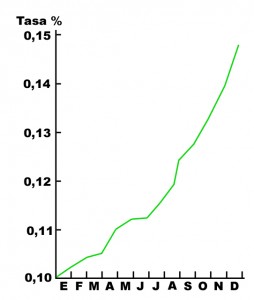
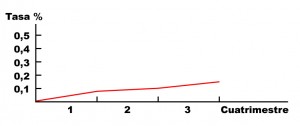
Para cerrar el apartado de fraudes veamos una triquiñuela muy habitual en la presentación de estadísticas: la manipulación gráfica. Los datos de una estadística se ofrecen a menudo en forma de diagramas lineales o circulares (de «quesitos»), cuadros, histogramas, cartogramas, dispersogramas, pictogramas. Es una presentación rápida y, con frecuencia, muy atractiva. Algunos procedimientos son bastante imaginativos pero también resultan fáciles de manipular. Los ejemplos son innumerables, así que veremos aquí el más corriente: el cambio de escala en un diagrama lineal cartesiano:

Los dos dibujos ilustran la misma realidad: el crecimiento económico de un país en el último año. Y los dos se han realizado partiendo de los mismos datos, proporcionados por una fuente que consideraremos neutral. Sin embargo, uno de los gráficos parece mostrar una subida notable de la economía, mientras que el otro más bien señala una subida lenta, casi un estancamiento. ¿Cómo puede ser? El recurso básico es un simple cambio de escala, pero hay otros detalles. Uno ofrece el tiempo en cuatrimestres, el otro en meses. Uno, además, presenta la línea en rojo «peligro» y el otro en verde «optimista». Uno de los gráficos es el oficial del gobierno; el otro lo ha dibujado la oposición. ¿Cuál es cuál?.

En general las representaciones gráficas de la estadística pueden maquillarse de mil maneras. A veces con procedimientos típicos de la publicidad: los resultados favorables suelen disponerse con mucho colorido y en un formato «bonito». Pero si se quiere presentar algo «molesto», la apariencia del dibujo será sosa y triste... No es exactamente un fraude, pero se intenta influir en el ánimo del observador con triquiñuelas ajenas a la información en sí misma.

2. PLANTEAMIENTO SESGADO

Orientar un estudio para que dé los resultados que queremos es cosa más frecuente de lo que se podría pensar. Se da en trabajos científicos donde el investigador organiza sus experimentos de forma que apoyen su hipótesis. Es decir, se busca de forma apriorística un resultado que fundamente la «verdad» buscada. Pero este es en realidad un punto fuerte del método científico: por mucho que el investigador se empeñe, otro científico querrá reproducir sus resultados y no será tan indulgente a la hora de pasar por alto los detalles que no corroboren la hipótesis. Por otra parte esta forma de sesgar un estudio puede ser también un contraste de la honradez del científico. Es célebre al respecto el caso de Robert Millikan, quien pasó diez años de su vida intentando rebatir los aspectos cuánticos de la teoría de Einstein sobre el efecto fotoeléctrico. Los resultados apoyaron obstinadamente las hipótesis del alemán y Millikan no dudó en reconocerlo.

Por desgracia la estadística sesgada no es siempre tan honesta, pero es muy corriente, a veces de forma inadvertida, a veces deliberada. En los años cuarenta y cincuenta del siglo XX se realizaron en Estados Unidos varios estudios para determinar la inteligencia media de los ciudadanos clasificados por razas, edades, sexos... Todo muy inocente, si no fuera porque muchas preguntas de la encuesta estaban orientadas de tal forma que sólo los blancos pudieran dar la respuesta correcta. ¿Cómo? Pues tampoco se comieron mucho la cabeza. Por ejemplo, en una casilla aparecían dos dibujos representando sendos rostros de mujer: uno de una chica joven, de rasgos finos y, aunque los dibujos no estaban coloreados, su aspecto era claramente el de una muchacha blanca (o caucásica, que dicen por allí). La otra figura mostraba a una mujer gorda, mofletuda, no demasiado joven y con los rasgos propios de la raza negra (o afroamericana, que dicen también por allí, por más que la mayoría de los negros de América no hayan pisado África en su vida, igual que los blancos no suelen visitar el Cáucaso). ¿Cuál era la pregunta? Había que indicar cuál de los dos rostros era más bello. Y como ya habrá adivinado el lector, la respuesta correcta pasaba por decir que la más guapa era la chica blanca. Este ejemplo, por más ridículo que parezca, es rigurosamente cierto y sirvió, junto a otros estudios parecidos, para apoyar la segregación racial en Estados Unidos, pues se había «comprobado científicamente» que los negros estadounidenses eran menos inteligentes que los blancos.

Esta forma de hacer las cosas tiene un nombre (aparte de «manipulación»): falta de base científica. La belleza de un rostro es subjetiva y nunca debería utilizarse como fundamento de un análisis estadístico serio. Otros ejemplos de estudios que se pretenden estadísticos pero no tienen base científica son las encuestas que una emisora de radio propone a sus oyentes o las que una marca hace a los compradores (sobre todo si las preguntas no se refieren exclusivamente a la emisora o al producto en venta).

A la hora de marcar un sesgo estadístico un procedimiento sencillo consiste en escoger mal la muestra, de forma que no sea representativa. Imaginemos una encuesta sobre intención de voto realizada exclusivamente en Puerta de Hierro (un barrio rico de Madrid), pero con la pretensión de que los resultados ofrezcan una predicción general de toda la población votante española. Si la muestra es grande (pero sin salir de ese barrio afortunado) el margen de error teórico será pequeño. Sin embargo, la encuesta no es fiable en ningún caso: es bastante seguro que ofrecerá pronósticos muy favorables a los partidos de derechas, por lo que esto no sería estadística, sino propaganda (salvo que la intención de la encuesta fuera la de mostrar la intención de voto en un barrio conservador, en cuyo caso sería legítima). Esta clase de tomaduras de pelo las encontramos a diario en todo tipo de medios.

El sesgo a veces aparece de forma inadvertida, incluso un tanto paradójica. Es un problema funcional de la estadística: a mayor pretensión de exactitud en una predicción (determinación del intervalo de confianza), menos fiables son los resultados. Si queremos predecir el resultado de unas elecciones a partir de un sondeo, tendremos que admitir siempre un margen de error, entre otras cosas porque antes de unas elecciones siempre existe un porcentaje grande de personas que no definen su voto hasta el final. Si una encuesta de este tipo pretende ser muy precisa, casi adivinatoria, tendrá que hacerlo a costa de «matizar» el margen de error. De hecho, si al final acierta será por pura casualidad. La experiencia nos demuestra, comicio tras comicio, que las encuestas pre-electorales no son muy de fiar.

El planteamiento sesgado en las conclusiones puede practicarse de manera muy sencilla ofreciendo los datos crudos, sin más aditivos. Por ejemplo, si se dice que Soria es la ciudad de España donde se producen menos atropellos y Barcelona donde más, esto no implica que Soria sea más segura que Barcelona para los peatones. El dato relevante sería la frecuencia relativa en cada ciudad. Lo único que se puede sacar en claro de la información primaria es que en Soria hay menos atropellos porque hay menos habitantes y menos vehículos que en la capital de Cataluña.

Dentro de las triquiñuelas de sesgo que más gustan a políticos y publicistas está la de ofrecer datos sin siquiera considerar el margen de error. Puede que el estudio se haya realizado de forma correcta, pero el personaje que ofrezca la información, sobre todo si le es favorable, quizá recurra a la industria de no presentar las variables completas. Por ejemplo, nuestro gobierno de turno sale a la palestra de nuevo para informar de otro logro: un crecimiento económico, el último mes, del 0,2 por ciento. No está mal, dentro de lo que cabe. No es para ponerse a tirar cohetes, pero es un dato positivo después de años de crisis. Ahora bien, ¿es realmente positivo? Depende de los datos generales de la economía (que el portavoz no ha citado) y del margen de error de la estadística (del que no ha dicho ni pío). Lo que ofrece el análisis estadístico es un abanico de resultados posibles dentro del margen de error calculado. El gobierno, al hacer su proclama, sólo habla del resultado más favorable posible. La verdad, seguramente, estará en otro punto. Y es incluso posible que la economía haya ido a peor.

Otro tipo de estadística sesgada es la que proporcionan los medidores de audiencia televisiva. Situados de forma aleatoria en domicilios particulares (¿alguien conoce a alguna persona que tenga en casa uno de estos aparatos?), los resultados son de gran importancia para las empresas televisivas y publicitarias. ¿Cuál es su grado de fiabilidad? Tal vez no tanto como se pretende. El aparato sólo registra si la televisión está encendida o apagada y, en el primer caso, en qué canal se ha sintonizado. No indica el grado de atención del telespectador ni el número real de personas que están viendo ese receptor concreto. Todos dejamos, muchas veces, la tele encendida, en ocasiones durante horas, sin mirarla ni un instante. También es habitual aprovechar las interrupciones publicitarias para preparar un bocata, ir a mear o estirar las piernas. ¿Y qué pasa si hay dos o más televisiones en la casa?
Para terminar: no hay que confundir el «sesgo estadístico» con la estadística sesgada. Lo primero es una fórmula bien definida que sirve, precisamente, para tratar de determinar hasta qué punto un estudio se encuentra sesgado por algún parámetro. La estadística cien por cien objetiva no existe, o es, desde luego, muy rara.

_________

Y aquí lo dejo, de momento. Próximamente la segunda parte de «Las triquiñuelas de la estadística», donde continuare con errores de interpretación, falacias y paradojas que espero que hagan las delicias de los lectores.