6 febrero 2014

Seguir a @pmarsupia
[caption id="attachment_9124" align="aligncenter" width="590"]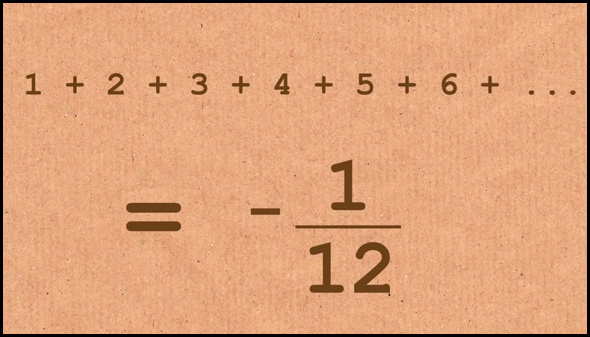 Crédito de la imagen: Youtube[/caption] Pregunta: ¿Cuánto da la suma de TODOS los números POSITIVOS?

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ... = ?

(Los puntos suspensivos significan que tenemos que sumar todos los números positivos hasta el infinito) Será un número enorme, enorme, enorme, ¿verdad? Respuesta correcta: -1/12, ¡¡¡un número NEGATIVO!!! Este resultado no es sólo matemáticamente cierto. Además, resulta necesario en muchos campos de la física: desde la teoría de cuerdas hasta la mecánica cuántica. Y sí, la primera vez que encontré esto en un libro de matemáticas casi me estalla la cabeza. ¿Cómo puede ser que la suma de todos los números positivos dé un número negativo?

****

Una pequeña introducción

Las sumas (que también se llaman "series") de infinitos términos son uno de los objetos más estudiados en matemáticas. Básicamente existen dos tipos: a) Las series convergentes, que tienen un valor bien definido. Por ejemplo:

1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + .... = 2

Os puede parecer algo extraño, pero una suma de infinitas fracciones como esta tiene un resultado finito. Sería imposible realizarla incluso con un ordenador porque tiene infinitos términos y no acabaríamos nunca. Pero las matemáticas son maravillosas y es muy sencillo demostrar que el resultado es 2. Por cierto, este ejemplo muestra que la paradoja de "Aquiles y la tortuga" inventada por el filósofo griego Zenón no es tal. b) Las series divergentes, que, en principio, no tienen un valor definido. La serie que nos interesa es divergente. Dicho en términos técnicos: "la sucesión de sumas parciales tiende al infinito":

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 +... = ?

Pero resulta que sí podemos asignarle un valor matemáticamente riguroso a esta suma y que ese valor es -1/12.

****

Euler y más tarde Riemann nos enseñaron que podemos extender de forma rigurosa y consistente el concepto de "suma" para las series divergentes. En nuestro caso, basta con sustituir la serie original por una de Dirichlet y luego calcular por continuación analítica cierto valor de la función zeta de Riemann para obtener el valor -1/12. Una forma mucho más sencilla de entenderlo es a través del método que utilizan en este vídeo Brady Haran, y Antonio Padilla, un físico de la Universidad de Nottingham. (NOTA: En el vídeo se realizan algunos pasos que no son matemáticamente rigurosos, pero aún así, resulta muy interesante desde un punto de vista pedagógico). http://www.youtube.com/watch?v=w-I6XTVZXww Como decía Niels Henrik Abel, otro de los grandes de las matemáticas:

"Las series divergentes son una invención del diablo".

Quienes queráis más detalles técnicos sobre el resultado, podéis consultar estas notas en pdf. Seguir a @pmarsupia